| 用 語 |
説 明 |
| v-f 比 |
べん毛回転数に対する遊泳速度の比。べん毛が1回転する間に細胞が進む距離でもある。ワインのコルク抜きのように媒体に対して滑らなければ1ピッチの長さになり、反対にその場で回転するだけであれば0である。したがって、この値はべん毛の推進効率であると言ってもよい。 |
| 抵抗力理論 |
物体を小さな部分に分割し、それぞれが独立に流体中に存在するとして得られた流体力を総合し、物体全体に働く流体力を求める方法。近似解法だが、細菌運動などレイノルズ数の小さな世界における解析において有効である。 |
| 粘性 |
静止している流体の中に任意な平面を考えるとき、その面を通して両側の流体部分におよぼす力は常に面に直角で、法線応力は存在しない。しかし運動している流体では、隣り合った流体の部分が異なる速度で流れている場合、速度をならして一様にするような向きの法線応力が現れる。この性質を流体の粘性という。(岩波理化学辞典より) |
| 粘度(粘性率) |
流体の速度が流れの各点で異なる場合、粘性のために速度の勾配に比例する接線応力が現れる。すなわち、流体がx軸に平行に流れ、速度uがy方向に変化するとき、y軸に垂直な面にはXy=μ・du/dyの大きさの接線応力が現れる(ニュートンの粘性の法則)。比例係数μは流体によって定まる物質定数で粘性率という。(岩波理化学辞典より) |
| べん毛 |
細菌の運動器官。細胞の外側に存在するらせん形の構造物をべん毛繊維、その根元にある構造をべん毛モーターという。真核生物の鞭毛と違い、べん毛繊維そのものは運動性がない。回転力を発生するのはべん毛モーターであり、そのエネルギー源はATPではなく、細胞内外の間に維持されているプロトンやナトリウムイオンの電気化学ポテンシャル差(膜電位差+イオン濃度差)である。 |
| レイノルズ数 |
流れを特徴づける代表的な長さをL、速度をu、動粘度をν(粘度/密度)とすると、R=Lu/νで表される無次元数。流れの慣性項と粘性項の比に対応し、遅い流れでは小さな値になる。 |
| レプテーションモデル |
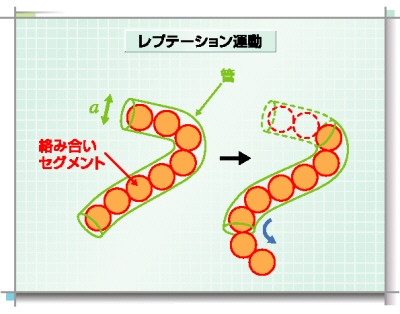
絡み合いを表す管状領域中の Rouse 直鎖を考えます。Doi-Edwards 模型は、この管が固定され、管に沿って測った鎖の長さは一定であると仮定(近似)します。固定管の仮定は、注目している鎖の周囲の鎖(管を形成している鎖)の運動が非常に遅い場合に成立します。また、鎖長一定の仮定は、注目している鎖が非常に長い場合に成立します。絡み合い鎖の大規模運動は、絡み合い点間分子量
Meを持つ部分鎖を単位として記述されます。この部分鎖を絡み合いセグメントと呼びます。Doi-Edwards
模型では、この絡み合いセグメントの大きさに等しい直径 a を持つ固定管を考えます。この管中に拘束された一定長の鎖は、管軸に沿って全てのセグメントが協同的に拡散することによってのみ、大規模な運動を起こします。この協同拡散運動をレプテーションと呼びます。(CD-ROM工学系基礎教材「高分子物性」より)
 |
