| 前の記事 | | | 目次 | | | 研究所 | | | 次の記事 |
Correlated z-values and accuracy of large scale statistical estimates.
Bradley Efron
Journal of the American Statistical Association 105(491), 1042-1055 (2010)
近年になって、大規模なデータが比較的容易に手に入れられるようになり、一昔前には考えられなかったような数の要因の比較を同時に行うケースが見られるようになった。たとえば、マイクロアレイデータや１塩基変異 (SNPs) と疾患との関係を調べるために、ゲノムワイドで、数千の遺伝子、数百万の SNPs を一度に比較する研究が行われている。このような場合には、たとえ単純な２群間の比較であったとしても、従来と同じ統計手法では太刀打ちできないことも多くなってくる。大規模データの解析において、推定、検定、予測を行うための統計手法を開発することはホットなトピックとなっている。農業環境分野でも、効率的な育種や遺伝的な多様性の評価などにおいて、このような研究が増えている。
たとえば、ある疾患の発生と遺伝子頻度の関係を調べる場合、数千の、場合によっては万を超える数の遺伝子の頻度と疾患の発生率を比べることになる。その場合、各遺伝子が要約統計量をひとつずつ持つことになる。たとえば平均からの距離を標準偏差の倍数で表す「 z 値」を利用する統計処理は、各 z 値が互いに独立であるという仮定の下で構築されているが、その仮定は実際には現実的ではない (Owen (2005) ,Efron (2007a))。この論文では、急性リンパ芽球性白血病 (ALL) と急性骨髄芽球性白血病 (AML) の患者グループで 7,128 個の遺伝子を比較する際の、それぞれの遺伝子に対応する z 値の分布を例として、データを解析する際に使用する要約統計量が互いに独立でない場合に推定が不正確になってしまう問題を調整する際の対処法について報告している。
論文の内容は以下のように要約される。
(1) 正規性の導入
もし、各遺伝子が独立であるならば、理論的には z 値の分布は N(0,1) の正規分布で近似できるはずであり、その分布において極端に大きな（小さな）z 値を持つ遺伝子が、疾患に特異的な遺伝子とみなされるが、上述の２群間の z 値の分布を正規分布で近似した分布 (empirical null distribution) と、得られたヒストグラムをスムージング手法で近似した分布とを比較すると、両裾（すそ）の部分で大きな相違が見られた。しかし、近似した分布を平均と分散の異なる正規分布の混合分布とみなすことで、各 z 値間の相関による推定の正確性を評価する上で、正規分布の性質を利用することができる。
(2) ペナルティの近似
z 値の分布の累積分布関数の分散は、累積分布関数の二項分散と相関によるペナルティ項という形に書き下すことができる。各 z 値が独立であればあるほど、ペナルティ項はゼロに近づく。このペナルティ項を正確に記述すると、N 個の z 値の場合、N × ( N - 1 ) / 2 の共分散行列に基づいて決定されることになるが、非常に複雑な計算を要する。しかし、ここで N が非常に大きいことによって、1 / N がかかる項をほぼゼロとみなすことができ、さらに著者らが提案する二乗平均平方根相関 （Root mean square correlation ＝ RMS 相関）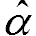
によって近似することができ、計算が簡略化できる。
(3) 白血病のデータとシミュレーションによる検証
ALL と AML のデータセットから、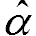と混合分布のパラメータを推定する。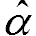の推定は、力わざで計算するほかに、ランダムサンプリングによる推定も行われている。分布の混合については、ヒストグラムの各位において、local fdr （偽発見率） がどの程度かに基づき、本当に有意な差があると考えられる z 値の数の期待値をヒストグラムに重ね描きする方法 (Efron 2007b) を用いて、今回用いた白血病データは３つの正規分布の混合とみなし、それぞれの正規分布がデータに占める割合、平均、分散を推定した。これらの結果にもとづいて z 値の分布の持つ標準偏差を推定したところ、z 値がゼロ付近で標準偏差が低くなる二山形の分布が得られ、z 値間の相関を無視した推定、検定が非常に危険であることが示唆された。
(4) その他の要約統計量への拡張
累積分布関数について得られた結果を、近似法のひとつであるデルタ法を用いて、それ以外の q 次元のカウントベクトル関数の共分散推定に拡張しても機能することを示した。
(5) t 値の分布の正規分布への近似
t 値の分布が、歪度（わいど）や尖度（せんど）のパラメータを持った分布となる場合について、ガンマ分布や非心 t 分布についても近似的に正規分布として扱えることを示し、今回報告された方法論を利用することが正当化できるとしている。
今回紹介した、データ間の相関などの計算量の問題以外にも、データが大規模であることそれ自体が、さまざまな問題を引き起こす。コンピュータの発展に伴い、処理速度は向上してはいるが、大量のデータを利用する分野では、今後、推定方法自体の簡略化や効率的なアルゴリズムの開発などが必須になってくると思われる。
引用文献
Efron, B. (2007a). Correlation and large-scale simultaneous significance testing. J. Amer. Statist. Assoc. 102: 93-103.
Efron, B. (2007b). Size, power and false discovery rates. Ann. Statist. 35: 1351-1377.
Owen, A. B. (2005). Variance of the number of false discoveries. J. R. Stat. Soc. Ser. B Stat. Methodol. 67: 411-426.
（生態系計測研究領域 大東 健太郎）