| 前の記事 | | | 目次 | | | 研究所 | | | 次の記事 |
前回はデータセットの “ばらつき” はどのようにして数値化できるかについて説明しました。複数のデータのそれぞれは 「平均」 という基準点に対する「偏差」によって “ばらつき” が求められます。それらの偏差の集計値である 「(偏差)平方和」 を計算すれば、単一の数値によってデータセット全体のばらつきを表現できる尺度となります。この結論から今回の話はスタートします。
上のようにして得られた平方和の視覚的イメージをまずはじめにお見せしましょう。ある花の 「花弁幅(Sepal.Width)」 と 「花弁長(Sepal.Length)」 を 150 標本について計測したデータセットがここにあります。このデータセットをそれぞれの計測データごとに1ミリメートル単位で図示したのが 図1 です。ここに用いたグラフは 「蜂群図(bee swarm plot)」 と呼ばれ、各データ点(丸印)がどのようにばらついているかを点が積み上がる “高さ” によって視覚化します。丸印が高く積み上がった箇所は高頻度を意味します。
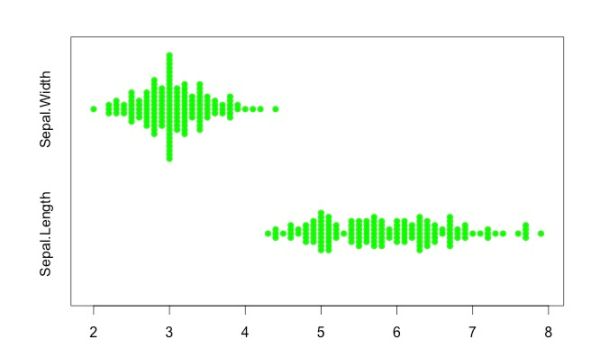
センチメートル単位で表される横軸に沿って、この二つの計測データセットがどのようにばらついているかが一目で視覚化できます。実際に平均と平方和を計算すると次のようになります。
花弁幅(Sepal.Width) :平均 3.06、平方和 28.31
花弁長(Sepal.Length):平均 5.84、平方和 102.17
実測値では平均の位置がそれぞれの蜂群図で異なります。いま、平均がゼロになるようにデータをそろえる(「センタリング」する)と、次の 図2 のようにもっと見やすい図になります。
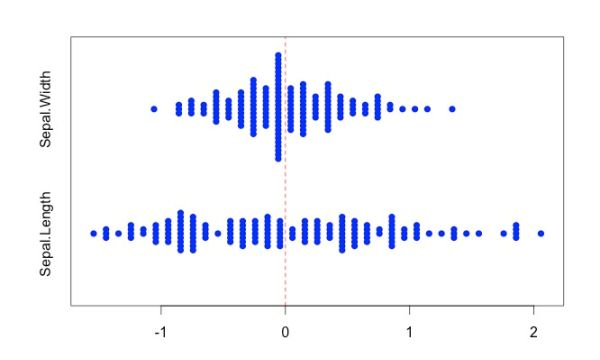
センタリングした結果、それぞれの計測データセットは平均値ゼロ(赤の破線で示す)になります。平方和の値はセンタリングしても変わらないので、 各データセットの平方和がより直感的に理解しやすくなりました。データセットの平方和の大小はデータが平均からどれくらい遠くまでばらつくかの視覚イメージとうまく連動しています。平方和がより小さい花弁幅データセットは、平方和がより大きな花弁長データセットよりも、平均まわりの狭い範囲にばらつきが限られていることがわかります。
このように二つのデータセットが同数のデータを含んでいるときには、上で説明したように、直感的にわかりやすい結果になります。ところが、前回の最後に提起したように、データセットによってデータ数がちがっているとき、すなわち「データサイズ」が異なっていると話は別です。
図2 の二つのデータセットはともに 150 個という同数のデータを含んでいます。ここで、花弁長データ 150 から無作為にデータ点を抽出するという操作をしてみます。たとえば、元の 150 個から 50 個を無作為抽出するすなわちデータサイズを3分の1に減らす操作を数十回繰り返すと、平方和の平均値はおよそ 35 になります。元データの平方和は 100 を越えていましたから、データサイズが減少すると平方和はそれにともなって減るということです。
削減率をさらに強めて、花弁長 150 個から 30 個を無作為抽出する操作を反復すると、平方和の平均値はおよそ 20 前後にまで減少します。一方、それよりも5倍のデータサイズがある花弁幅データ 150 個の平方和は 28 程度であることを考えると、データサイズを減らすことにより、平方和の値が “逆転” する現象が生じることが示唆されます。
データサイズが異なるときに生じ得る、平方和の大小関係の “逆転” を模式的に示したのが 図3 です。
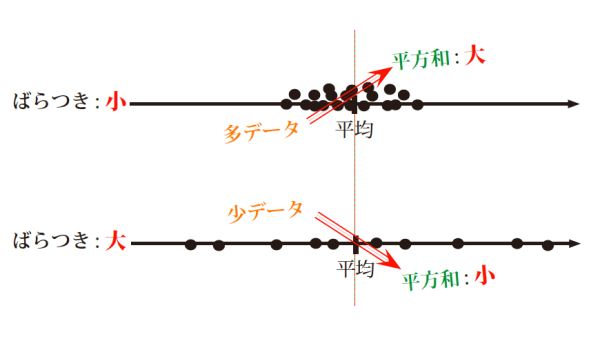
上の図は、サイズの大きなデータセットが平均まわりのごく狭い範囲に集中して分布する状況、すなわち “ばらつき” が小さいと認知される場合を示しています。一方、下の図は、サイズの小さなデータセットが平均から遠くまで分散している状況、すなわち “ばらつき” が大きい場合を表しています。データサイズのちがいを考慮してもなお、認知的な “ばらつき” の大小は明確に判断できるでしょう。ところが、平方和をそのまま “ばらつき” の数値的尺度とみなすと、上で計算したように、サイズの小さなデータセットの方がたとえ “ばらつき” が大きいように見えてもその平方和がより小さくなる可能性があります。
このような “逆転” が生じる原因は平方和のもつ基本性質にあります。平方和は個々のデータがもつ偏差の平方をデータセット全体にわたって足し合わせて求めます。平均まわりのごく狭い範囲にデータの分布が集中しているとき、ひとつひとつの偏差(の平方)は小さな値であったとしても、データサイズが十分に大きければ総和としての平方和の値はより大きくなるでしょう。一方、平均から遠くにまで散らばっているデータセットの場合、たしかに個々の偏差(の平方)は大きな値を取るでしょうが、データサイズが小さいならば、集計した平方和としてはデータサイズが大きくしかも集中分布をするデータセットにはかなわないかもしれません。
つまり、データサイズのちがいを考慮しないという点で、平方和はデータの “ばらつき” の数値尺度として大きな欠陥をもっているということです。では、複数のデータセットの “ばらつき” を互いに比較するとき、データサイズのちがいをどのように補正すれば、より “公平” な比較が可能になるのでしょうか。
高校数学「確率・統計」の検定教科書に書かれているやり方は、平方和をデータサイズで割り算するという方法です。たとえば、ふたつのデータセットのサイズがそれぞれ 10 と 100 であったとき、各データセットから計算された平方和を対応するデータサイズで割り算することで “補正” するわけです。この方法は直感的にとてもわかりやすいという利点があります。平均を計算するときに、データの総和をデータサイズで割り算するのとまったく同じやり方で、偏差の平方和をデータサイズで割り算すればいいからです。
データサイズで割り算すると不適切な結果をもたらす簡単な数値例をお見せしましょう。図4 は、“ばらつき” の値が正確に 「1.0」(緑色の線の位置) であることがわかっている無限個のデータ集団から、無作為に10個のデータを抽出するというシミュレーションを千回繰り返し、得られた千個の平方和をデータサイズ10で割り算した値 (図中の「var.biased」) のヒストグラムとその平均 (赤色の線の位置) を図示したものです。縦軸は頻度(density)を表しています。
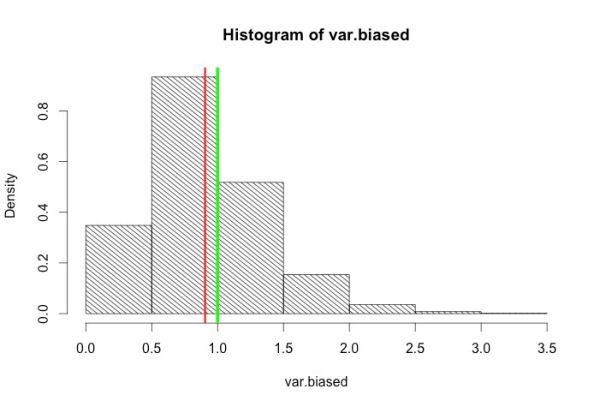
すぐわかるように、平方和をデータサイズ 10 で割った値は真の値 1.0 よりも小さくなります。すなわち、「平方和÷データサイズ」 という “補正法” では、この実験で最初に与えた “ばらつき” の真の値を正しく導くことはできません。
実は、ここで私たちは統計的思考の次なるステージへの一歩を踏み出しています。それは何のために平均や平方和を計算するのかという統計学の根幹に関わっています。たとえば、目の前に 10 個の数字(データ)があるとき、そのデータの特徴を集約する目的で平均を計算したり、平方和を求めたりすることができます。これは 「記述統計学」 的な統計計算の考え方です。記述統計学が目指すところは、データの特性や挙動を数値的に描き出すことです。そして、記述統計学の世界にとどまるかぎり、データセットの “ばらつき” をそのサイズによって補正することには何も問題はありません。
ところが、上の数値シミュレーションは、記述統計学ではなく、「推測統計学」 という別の目的をもった統計学に属しています。推測統計学とは観察者の目の前にあるデータの背後に広がる 「母集団」 に関する推測を行なうための方法論を指しています。上のシミュレーションをもう一度見ると、記述統計学と推測統計学とのちがいがはっきりします。ここで想定している 「母集団」 とは “ばらつき” の値が1.0であることがわかっている無限個のデータの集まりです。そこから無作為に 10 個のデータ (サンプル=標本)を抽出するという操作をしています。私たちの目的は、この有限個の標本(データ)から母集団の “ばらつき” に関する推定をしようというのがここでの推測統計学のゴールになります。一方、記述統計学は目の前の 10 個の数値データの集約をするだけで、背後の母集団に関する推論は眼中にありません。
平方和をデータサイズで割るという計算は、たとえ記述統計学的には妥当であったとしても、推測統計学的には母集団の “ばらつき” に関する正しい推定値を導きません。それでは、推測統計学の観点からみて平方和の妥当な “補正法” とは何かが次の問題になります。
母集団から無作為に抽出された標本(データサイズをnとしましょう)は互いに無関係(統計学では「互いに独立」と呼びます)なので、平均を計算する際にデータの総和をデータサイズnで割り算して “真ん中” を決めるのはまったく問題ありません。
しかし、平方和の場合はそうはいきません。前回説明したように、無作為抽出された標本から計算された偏差の総和はゼロになってしまいます。したがって、n個のデータから計算されたn個の偏差のうち、いずれかひとつは他の n−1 個の偏差によって決定されてしまいます。見かけはn個の偏差がありますが、実際に “自由” に値がとれる偏差は n−1 個しかありません。この 「n−1」 という値は平方和がもつ 「自由度」 と呼ばれます。要するに、平方和をデータサイズnで割るのは “割り過ぎ” ということです。図4 が示すように、「平方和÷データサイズ(n)」 が真の値に対してつねに 「過小推定」 の傾向がある原因はここにあります。
推測統計学的に妥当な平方和の “補正法” は「平方和÷自由度(n−1)」であることが証明されているのですが、ここでは上の数値シミュレーションをそのまま使ってその妥当性を示しておきましょう。次の 図5 は、図4 の 「平方和÷データサイズ」 に加えて、「平方和÷自由度」 のヒストグラムとその平均値を青の線で記入したものです。
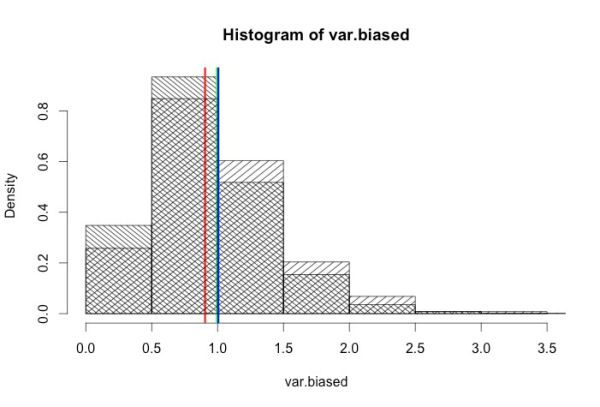
見ればすぐにわかるように、平方和を自由度で割った値(青色)は真値(緑色)とほぼ重なっていて、妥当な推定をしていることがわかります。平方和をその自由度で割った値を 「不偏分散」 と呼びます。私たちは、抽出されたサンプルデータからこの不偏分散を計算することにより、背後の母集団に関する推測をしているのです。
三中 信宏 (生態系計測研究領域)
■農環研ウェブ高座「農業環境のための統計学」 掲載リスト
第1回 前口上−統計学の世界を鳥瞰するために (2012年8月)
第2回 統計学のロジックとフィーリング (2012年9月)
第3回 直感的な素朴統計学からはじまる道 (2012年10月)
第4回 統計学的推論としてのアブダクション (2012年11月)
第5回 データを観る・見る・診る (2013年1月)
第6回 情報可視化と統計グラフィックス (2013年2月)
第7回 データのふるまいを数値化する:平均と分散 (2013年3月)
第8回 記述統計学と推測統計学:世界観のちがい (2013年4月)
第9回 統計モデルとは何か:既知から未知へ (2013年5月)
第10回 確率変数と確率分布:確率分布曼荼羅をたどる (2013年6月)
第11回 正規分布帝国とその臣下たち (2013年7月)
第12回 パラメトリック統計学の世界を眺める (2013年8月)