前の記事

|

目次

|

研究所

|

次の記事

農環研ウェブ高座 「農業環境のための統計学」 第９回 「統計モデルとは何か：既知から未知へ」

今回から 「統計モデル」 の話題に入ります。最近の統計データ分析では、コンピューターの計算能力が飛躍的に向上したことと、さまざまな統計解析ソフトウェアの開発が進展したことにより、かつてよりも格段に複雑な統計モデルを用いてデータ解析をすることが可能な時代になりました。これは多くの統計ユーザーにとって基本的には歓迎すべき状況です。しかし、その一方で、統計モデリングの技法もまた着実に高度化し、最尤法やベイズ統計学を駆使した先端的な統計モデルを使いこなすためにユーザー側に要求されるハードルもまた高くなりつつあります。

統計モデルの本論に入る前に、前回 「記述統計学と推測統計学：世界観のちがい」 の復習をしておきましょう。前回の話の要点は、データを解析する立場としての 「記述統計学」 と 「推測統計学」では根本的なちがいがあるということでした。たとえ同じ “観測値” を見ていても、基本的な問題設定と具体的な目標が異なるために、両者の間で手順と方法に差が生まれます。記述統計学のゴールは、目の前にあるデータセットの様相（パターン）の理解にあります。記述統計学で平均や分散などの統計量を用いる唯一の意義はデータのふるまいを要約することです。一方、推測統計学では、観測されたデータセットは背後に潜む仮想的な母集団からの無作為標本であるという仮定がされます。そして、データから計算される平均や分散などの統計量は、母集団を特徴づける母数（パラメーター）すなわち母平均や母分散を推定するための 「推定量（estimator）」 という新たな役割を担います。

推測統計学における推定量は、単にデータを “要約” するだけでは資格不十分で、母数をきちんと正しく推定できるかどうかのパフォーマンスが問われます。前回挙げた分散の推定の例を思い出しましょう。記述統計学では平方和をデータ数（ｎ）で割ろうが自由度（ｎ−１）で割ろうが本質的なちがいはありません。データのふるまいを集約するという目的を設定するかぎり、ｎ と ｎ−１ の差はデータ数が十分に大きければ実質的な差はなくなるからです。ところが、推測統計学ではそうはいきません。平方和÷ｎ という統計量は母分散の真の値に対してつねに 「過小推定」 というバイアスの弊害があるのに対して、平方和÷（ｎ−１） という統計量は母分散により近い推定値を一貫して与えるからです。平方和÷（ｎ−１） が母分散の 「不偏推定量」 と呼ばれる理由は過小推定バイアスがない点にあります。このように推測統計学は記述統計学とは別のゴールを設定します。

極端な例として「全数調査（悉皆（しっかい）調査）」というケースを考えてみましょう。全数調査とは文字通り母集団のすべての調査対象を調べつくすことです。このとき、母集団からの標本抽出は原理的にありえません。全対象を調べあげているわけですから、有限個の標本の無作為抽出という概念そのものが不要になるということです。また、記述統計学は全数データの要約という任務を担うことができますが、推測統計学は全数調査ではもはや出番がありません。母集団をすべて調べつくしたので、推定すべき母数そのものが消滅してしまったということです。

全数調査のような場合には推測統計学がそもそも適用できないという事実は、今回のメインテーマである 「統計モデル（statistical model）」 の問題と深く関わってきます。連載の第４回 「統計学的推論としてのアブダクション」 では、有限個の観察データという既知の情報に基づいて、背後の母集団の未知のパラメーターに関する非演繹的推論 （「アブダクション」） を行なうための手段が、統計学における 「モデル」 であると述べました。すなわち、抽出された標本 （サンプル） のふるまいを支配していると仮定される母集団の一般的規則性を明示化したものが 「統計モデル」 だということです。

既知から未知への跳躍をもくろむアブダクションには 「心理的本質主義」 の発動が求められます。観察データをじっと見つめる私たちは、既知の情報断片を何とかうまくつなぎあわせて未知の説明原理や法則性を導出しようとします。運よくデータを “きれいに” 説明できるモデルが構築できる見込みがあるならば、そのとき私たちは現実世界での観察データを支配する不可視の “本質” をつかむことができたという信念をもつでしょう。この意味で、統計モデルは人間のもつ心理的本質主義を映す鏡であるということができます。

しかし、この心理的本質主義を含めて、私たちがだれでももっている生得的な認知的傾向は統計的思考にとってプラスの面とマイナスの面をあわせ持っています。観察データを見たり、統計モデルをつくったりするときに私たちの “心（直感）” が正しく作動すれば問題はありません。しかし、第３回 「直感的な素朴統計学からはじまる道」 で言及したような 「第一種過誤」 という判断ミスを犯すリスクが私たちにはつねにあります。それはいわば私たちの心が意図しない “誤作動” と言うべきまちがいです。

これから統計モデルをつくろうとする私たちもまた同様の認知的バイアスの危険性がついてまわることを理解する必要があります。そのリスクを疑似体験していただくために、以下ではいくつかの事例をお見せしましょう。図１ は０以上１以下の実数 10 個を等確率で無作為に抽出し （「一様乱数」 と呼ばれます）、それを「□」 印で図示しました。横軸の 「obs」 は抽出された乱数を表します。

図１ 10 個の一様乱数 (1)

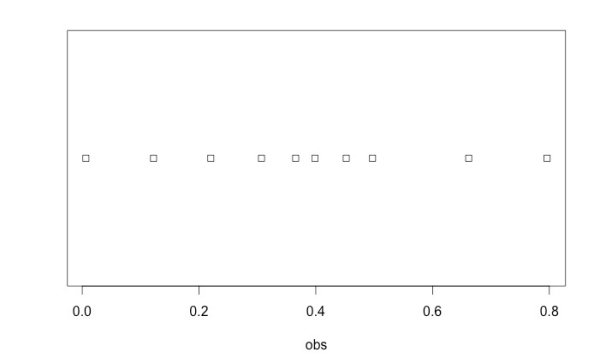
このように一様乱数を 10 個抽出する試行は毎回異なる結果を生み出します。たとえば、次の 図２ も一様乱数抽出のある試行の結果です。

図２ 10 個の一様乱数 (2)

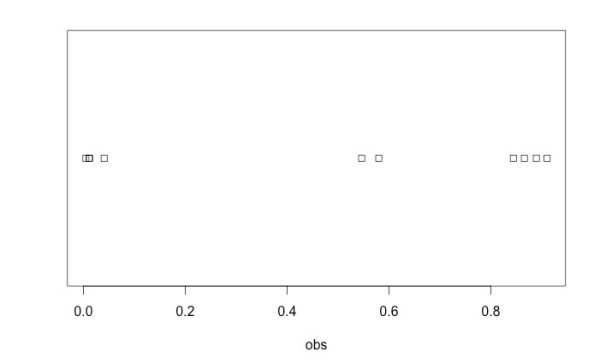
一様乱数データから私たちが直感するそのような規則性や因果性はすべて “まぼろし” です。それらのデータの背後にある母集団は０から１の範囲で等確率に存在する実数集合であると前提しているからです。したがって、無作為抽出された 10 個の実数間にはまったく何の関連性もありません。それにもかかわらず、私たちは目の前にある有限個の観察データの背後には 「何かあるにちがいない」 という心理的本質主義を誤作動させ、実在しないはずの規則性や因果性が 「ある」 と誤判断する第一種過誤をうっかり犯してしまいます。

数直線の一次元データではなく、平面の二次元データの例をお見せしましょう。図３ は二組の一様乱数を 20 個抽出し、それぞれの乱数の数直線 （横軸「obs1」と縦軸「obs2」） がつくる平面上に図示したものです。

図３ 20 個の二次元一様乱数 (1)

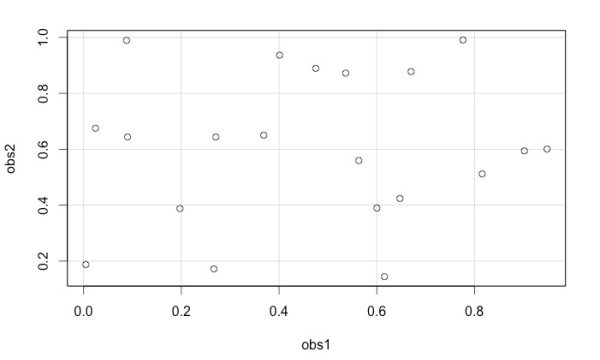
この 図３ を見てもとくに際立つ “パターン” は検出できないかもしれません。しかし、この抽出試行を繰り返すと、たとえば次の 図４ のようなケースが出現することがあります。

図４ 20 個の二次元一様乱数 (2)

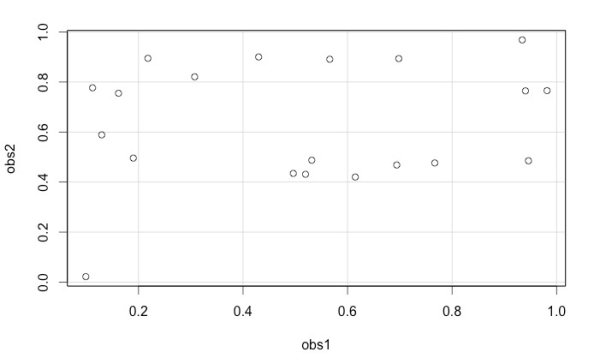
図４ を見た読者はある “パターン” を認知するのではないでしょうか。そのパターンとは第一乱数 「obs1」 が比較的まんべんなく分布しているのに対して、第二乱数 「obs2」 は 0.5 と 0.9 あたりに集中分布しているために生じる “水平線” の線形関係パターンです。

しかし、図３ と 図４ もまた母集団は一様乱数ですから、たとえ見かけ上の “パターン” が認知できたとしても、それは単なる誤解にすぎません。

以上、図１ − 図４ でお見せした例は、一般に 「ポアソン・クランピング（Poisson clumping）」 として知られている人間の認知心理的性向がどのように作動するかを示しています。ポアソン・クランピングとは、確率的に生じる無作為現象のなかに何らかの “非確率的必然” の存在を誤って読み取ってしまう人間の心理現象を指す用語です。第一種過誤を犯しやすい心理的本質主義者としてのヒトは容易にポアソン・クランピングの餌食（えじき）になってしまいます。

このような認知バイアスによる間違いの事例を列挙してしまうと、人間のもつ直感的能力に対して悲観してしまう読者がいるかもしれません。しかし、たとえ間違うリスクはあったとしても、人間の生得的認知能力がなかったならば、既知から未知への推論そのものができないこともまた事実であることをここで強調しておきましょう。

夜空にまたたくおびただしい数の星たちを私たちは 「星座」 という視覚的パターンとして認知してきました。もちろん、宇宙空間のなかでの実際の星の分布を考えるならば、地上から見上げた星座がそのまま空間的に隣接して並んでいるわけではありません。たとえば、夜空に柄杓（ひしゃく）の形を描く北斗七星を構成する星のうち六つは 50−80 光年の距離に分布していますが、もっとも遠いエータ（柄の先端の星）は 170 光年のかなたにあります。このように星座はあくまでも人間の目に映るみかけだけの “パターン” にほかなりません。しかし、星座の体系があればこそ、古代の天文学は発展し、近世の地理学や探検博物学は可能になったのです。

既知から未知へのアブダクションとしての統計モデリングに安全な王道はありません。私たちはいつもデータと対話しつつ試行錯誤を繰り返しながら “よりよい” 統計モデルをつくる地道な積み重ねが必要になるでしょう。それでもなお “完全無欠” の統計モデルがいつかはつくれるという楽観主義は禁物です。たとえよりよいモデルが構築できても “真実” のモデルはどこにもないのですから。推論の科学である統計学は真理を求めるタイプの科学ではけっしてありません。はてしない推論の連鎖をたどることにより、よりよい説明仮説へと改良し続けることが統計的データ解析の目標です。

三中 信宏 （生態系計測研究領域）