農環研ウェブ高座「農業環境のための統計学」第１１回 (農業と環境 No.159 2013.7)

私たちはやっとパラメトリック統計学という要塞（ようさい）の入り口に到達しました。見上げれば高くそびえ立つその威容は圧倒的です。その深奥部にいたるどの道をたどろうとも、すき間なく敷き詰められた数式や数学が登攀（とうはん）の意欲を萎（な）えさせます。いわゆる “数理統計学” を学んだことのある読者ならばきっと苦い思い出のひとつやふたつはあるにちがいないでしょう。しかし、ここではその悪夢を再現するつもりは毛頭ありません。むしろ、このパラメトリック統計学要塞の全容を上から見下ろしましょう。この要塞の基本構造をつかむには、地表から見上げるのではなく、上空から見下ろすのが効果的です。いずれはある道を踏みしめて登ることになろうとも、全体地図を知っていれば迷子になったり遭難したりするリスクはきっと減らせるでしょう。

今回の連載がスタートした初回に、統計学の世界を一望する「統計曼荼羅」を紹介しました。連載のゴールが見えてきましたので、その統計曼荼羅を今回は最初に示しましょう（図１）。

この図をあえて「マンダラ（曼荼羅）」と呼んだのは、統計学世界をかたちづくる個々の要素の間の錯綜（さくそう）した関連性を目に見えるように可視化しようとしたからです。博物学者・南方熊楠の世界観を「南方曼陀羅」と命名した鶴見和子は、「マンダラ」という図像のもつ性格について次のように述べました：「曼陀羅とは、『宇宙の真実の姿を、自己の哲学に従って立体または平面によって表現したもの』である。…［中略］…曼陀羅、今日の科学用語でいえば、モデルである。南方曼陀羅は、南方の世界観を、絵図として示したものなのである」（鶴見和子 1981. 南方熊楠：地球志向の比較学、講談社、pp. 82-84）。私の統計曼荼羅もまた統計学という広大な世界を視覚化するモデルのひとつとみなすことができるでしょう。また、記号学者ウンベルト・エーコは、百科事典的な知識の体系化には “迷宮（labirinto）” たる高次元ネットワークが必須であると主張しました（ウンベルト・エーコ 2007. 系統樹から迷路へ：記号と解釈に関する歴史的研究．ボンピアーニ、ミラノ）。統計学の “迷宮” を旅する私たちはつねにその大域的構造を見ぬくように心がけたいものです。

この統計曼荼羅に描いたように、統計学の世界はあまりに広すぎ、その詳細をつぶさに観察することはできません。私たちがいま登ろうとしているパラメトリック統計学要塞は、図の左の方に「由緒正しき正規分布帝国」と銘打たれたエリアにあります。農学や生物学をはじめとする応用分野で用いられているさまざまな伝統的統計手法の多くは、過去一世紀に及ぶパラメトリック統計学の歩みのなかで確立されてきました。母集団から抽出された標本に基づく推定や検定の原理と方法の構築はパラメトリック統計学が果たしたデータ解析へのきわめて重要な貢献です。高性能のコンピューターを用いた統計分析をだれもができるようになった現在でも、その重要性は損なわれることはありません。

これらの輝かしい成果の基礎となったのは確率分布に関する数学理論でした。データの挙動を数学的に記述するという前提から出発することにより、確率変数と確率分布は数値データの確率的挙動をモデル化することに成功しました。とりわけ、正規分布というひとつの確率分布が歴史的に重要な位置を占めている点を強調しておくべきでしょう。前回説明したように、統計学者カール・ピアソンは正規分布がいかに現実のデータのばらつきをうまく近似できているかを私たちに納得させました。

しかし、正規分布だけが確率分布ではありません。たとえば、ある一枚の硬貨を投げ上げるとき、表と裏の出る確率が等しく 0.5 であると仮定すると、全ｎ回投げたなかで表が出る回数ｘは「二項分布」という確率分布にしたがう確率変数になります（図２）。

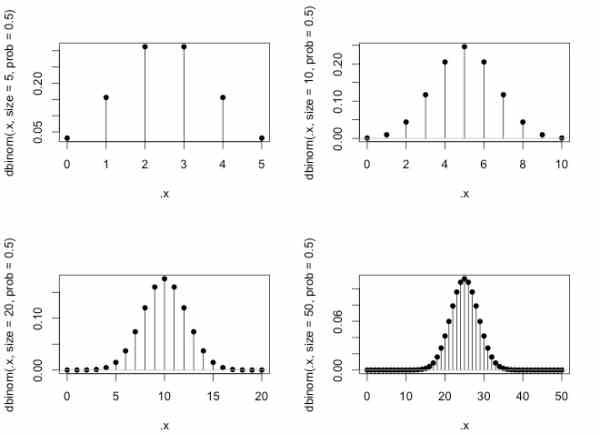
正規分布はすべての実数値を取り得る連続的な確率変数でしたが、この二項分布にしたがう確率変数は離散的な整数値しか取りません。

この世にはほかにも実にさまざまな確率分布がたくさんあるのです。では、いったいどれほど多くの確率分布がパラメトリック統計学の世界を形づくっているのでしょうか。その一覧をまさに「マンダラ」の形式で可視化した論文が数年前に発表されました： Lawrence M. Leemis and Jacquelyn T. McQueston 2008. Univariate Distribution Relationships. The American Statistician, volume 62, number 1, pp. 45-53。このチャート（図３「確率分布曼荼羅」）は現在フリーアクセスで読むことができます（ http://www.math.wm.edu/~leemis/chart/UDR/UDR.html ）。

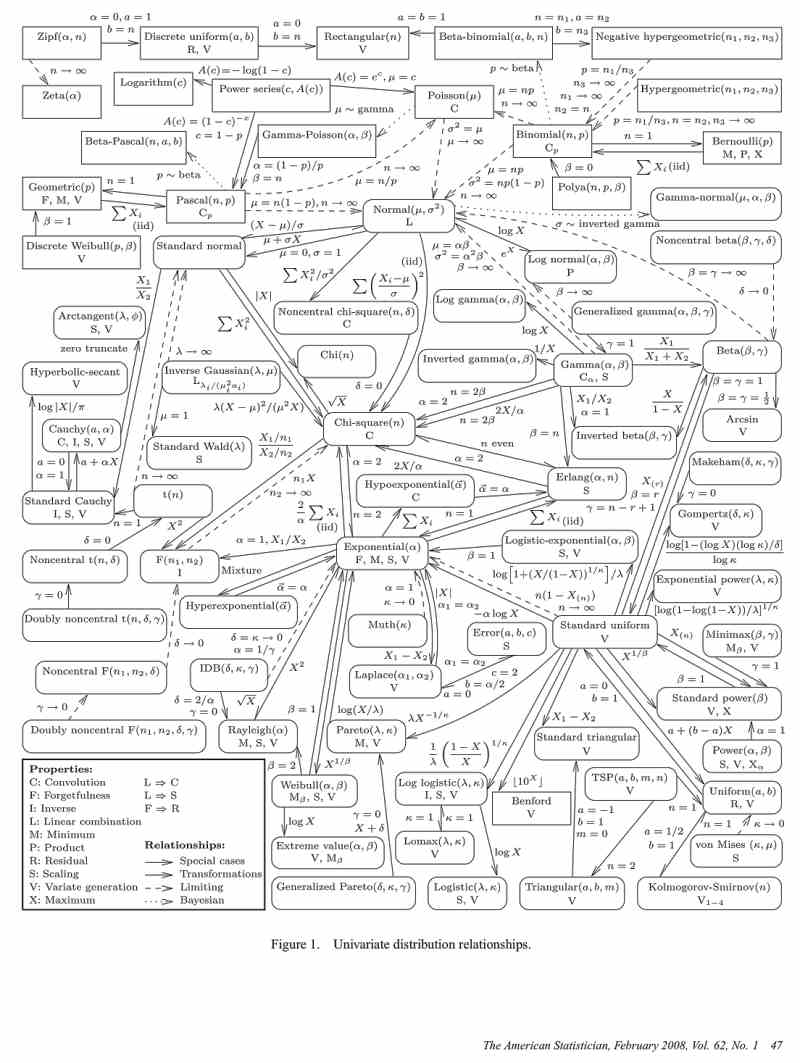
この確率分布曼荼羅には全部で 76 個の確率分布が掲載されており、その内訳は連続型（丸枠で囲まれた 57 個）ならびに離散型（四角枠で囲まれた 19 個）となっています。

予想をはるかに上回る数の確率分布がパラメトリック統計学においてすでに命名されていることにまず目を見張らされます。正規分布や二項分布のようなビッグネームもあれば、生物統計学が本職である（はずの）私ですら見たこともないような名前の確率分布さえあります。この論文はこれらの確率分布すべてを一枚の図によって可視化する試みです。

しかし、真に驚くべきことは、それらの確率分布の間に緊密な関連性が見出され、しかもその関係はすべて数学的に厳密な証明が与えられているという現実です。この堅固な基底こそ、パラメトリック統計学の要塞を難攻不落にしているのだと実感せざるを得ません。じっと見ていると目がチカチカしてくる確率分布曼荼羅ですが、読み解くポイントをいくつか設定しましょう。図の真ん中少し上に書かれている「Normal（μ，σ²）」とは正規分布を指しています。その右上に見える「Binomial（n, p）」は二項分布です。

この確率分布曼荼羅は、ある確率分布を出発点とするとき、その確率変数をどのように関数変換すればどんな確率分布が数学的に導出されるかを矢印によって接続し、全体として錯綜したネットワーク（すなわちマンダラ）を形成しています。このネットワーク構造の一部を拡大して説明しましょう（図４）。

図４確率分布曼荼羅（図３）の部分拡大図
赤でマークしたのは：「Normal＝正規分布」、「Standard normal＝標準正規分布」、「t＝ｔ分布」、「Chi-square＝カイ二乗分布」、「F＝Ｆ分布」。

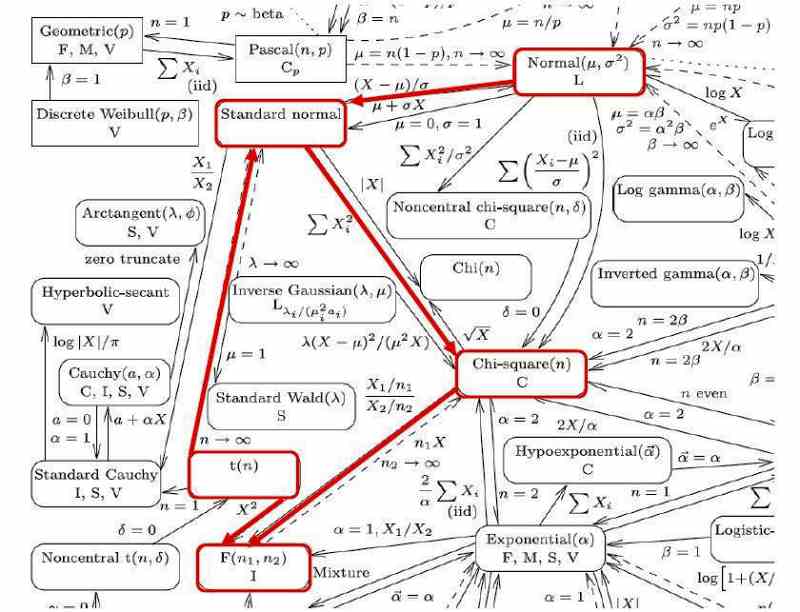
この図４でピックアップしたいくつかの確率分布の間の関連性を説明しましょう。平均 μ、分散 σ² をもつ正規分布（Normal）にしたがう確率変数ｘの一次変換 （x－μ）／σ は、平均０、分散１の標準正規分布（Standard normal）にしたがいます。標準正規分布をする確率変数の平方和はカイ二乗分布（Chi-square）にしたがい、独立なカイ二乗分布をする二つの確率変数の比はＦ分布にしたがうことがわかります。一方、標準正規分布の計算に用いた標準偏差 σ （分散 σ² の平方根）をそのサンプルサイズｎのデータからの推定値ｓで置換したｔ分布は、サンプルサイズｎを無限大にすると標準正規分布に収束します。さらに、ｔ分布をする確率変数の二乗はＦ分布にしたがうことになります。この確率分布曼荼羅のごく一部を拡大しただけでもこれだけの内容が詰め込まれているのですから、全体としていったいどれだけの情報量を含んでいるかは推して知るべしでしょう。

パラメトリック統計学の基礎にあるこれらおびただしい数の確率分布の中でも、正規分布は特異な地位を占めています。それは「中心極限定理（central limit therem）」と呼ばれる強力な定理のおかげです。この中心極限定理は、元の確率分布が何であれ、その母集団から抽出したデータから計算された標本平均はサンプルサイズが無限大になると標準正規分布をすることを証明します。

この中心極限定理がいかに強力であるかを示す一連の図をお見せしましょう。ここでは四つの確率分布（ Normal ＝正規分布、 Gamma ＝ガンマ分布、 Uniform ＝一様分布、 Beta ＝ベータ分布）を用います。各母集団からのサンプル回数は 10,000 個に設定します。次の図５が示すように、サンプルサイズが「1」すなわち各母集団からたったひとつのデータを抽出するという操作を 10,000 回繰り返してヒストグラムを描くと、それぞれの母集団の確率分布の形がそのままあらわれます。

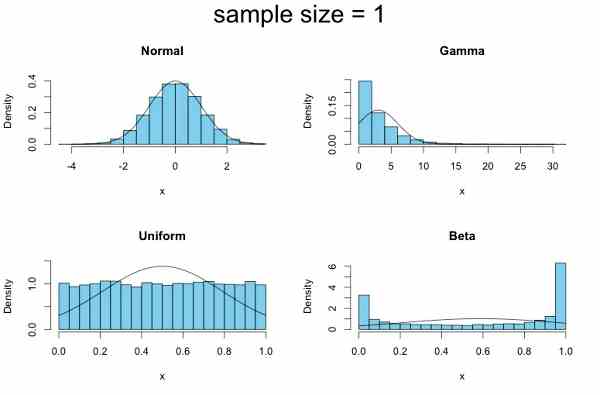
ところが、サンプルサイズを二倍の「2」にしたとき（図６）、大きな変化があります。

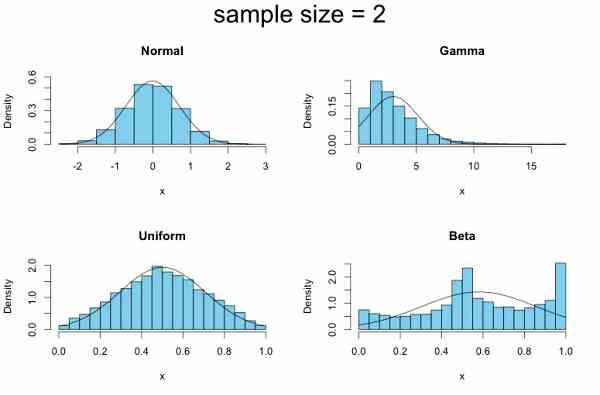
ことばで言えば、各母集団からふたつサンブルをとってその平均を求めるという試行を 10,000 回繰り返すと、サンプルサイズが「1」のときは平板だった一様分布が山形になり（下左）、真ん中がえぐれていたベータ分布は尖（とが）った山が中央部に出現します（下右）。さらにサンプルサイズを増やしましょう。

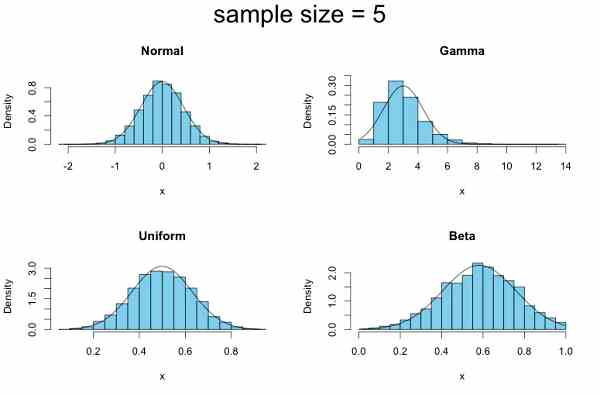
サンプルサイズを最初の五倍の「5」にすると、一様分布とベータ分布はもはや正規分布とほとんど見分けがつきません。ガンマ分布だけがしぶとく抵抗して非対称な形を保っています（上右）。しかし、サンブルサイズをさらに増やすとその抵抗もむなしく潰（つい）えます。

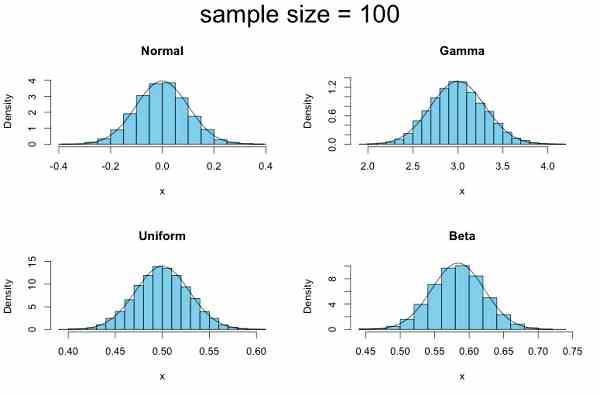
サンプルサイズを「100」にすると、最後までがんばったガンマ分布を含め、すべての確率分布の標本平均の分布は正規分布と識別できなくなることがわかります。つまり、元の確率変数の “出自” すなわち母集団の分布型が何であれ、サンプルサイズを十分にとるならばその標本平均は正規分布にしたがうとみなしてかまわない。これが中心極限定理の神託です。

私たちが統計データ解析をする際に、標本平均はもっとも重要な統計量のひとつです。サンプルサイズが増大するにつれ、この標本平均が正規分布に近づいていくという中心極限定理は、正規分布を “無敵” の確率分布に担ぎ上げるのに十分だったのです。私が統計曼荼羅の中で「由緒正しき正規分布帝国」と呼んだ理由はそこにありました。